Random distributions are not one-size-fits-all (part 2)

Updated 30.06.2024: I noticed a bug in the Java distribution implementation, which changed the performance profile. I reran the benchmarks and updated text below to reflect the reality.

In the previous post, we looked at Lemire's algorithm for generating uniformly distributed integers and how it can be specialized for different use cases. In this post, we will look at different algorithms for generating uniformly distributed random numbers and determine whether they fit specific use cases better than Lemire's algorithm.

Introduction

The original paper that introduced Lemire's algorithm compared it to two other algorithms, dubbed "OpenBSD" and "Java", based on the project they were taken from. Lemire's algorithm has won, by quite a lot. But when I was running the benchmarks for part 1, I noticed that when generating uint64_t, the expected differences decreased, or even disappeared entirely, due to the slow implementation of extended 64x64 -> 128-bit multiplication.

That got me thinking: Would Lemire's algorithm still win if we did not have access to hardware that has native support for 64x64->128 multiplication? Alternatively, how slow would the multiplication have to be for the implementations relying on modulo to win?

Let's first look at the different implementations of extended multiplication we will be using, and then we will look at the alternative algorithms for generating uniformly distributed random integers.

Extended multiplication

This post will benchmark three different approaches towards extended multiplication.

1. Naive
   This is the approach we all learned in elementary school as "long multiplication". Since we are working on a computer, we will use 32-bit integers as the individual digits. The advantage of this approach is that it is evidently correct and easy to implement.
2. Optimized
   You can find this approach floating around in places like Hacker's Delight. It also implements long multiplication, but unlike the naive approach, we do not keep to strictly 32-bit digits. This allows us to significantly reduce the number of additions that happen before we get the result. The advantage of this approach is that it is reasonably performant and also widely portable.
3. Intrinsic
   This approach uses the compiler intrinsic for extended multiplication. This leads to great results^[1] on CPUs that natively support 64x64 extended multiplication, but it is not available on all platforms, e.g. 32-bit x86 or ARM.

You can look at all of these on Compiler Explorer. When you look at the generated assembly, the optimized approach does less work than the naive approach. There is still the same total number of multiplications, but there are fewer additions, and fewer shifts and the critical chain is shorter.

Obviously, not all ASM instructions are equal, and counting them does not tell the whole story. So, we will benchmark all three approaches and compare their results later.

Alternative algorithms

Let's take a look at the pseudo-implementations of the two alternative algorithms.

OpenBSD

uint64_t openbsd(uint64_t max) {
    uint64_t threshold = (-max) % max;
    uint64_t x;
    do {
        x = random64();
    } while (x < threshold);
    return x % max;
}

As written, this algorithm needs to compute modulo twice per returned number, which virtually ensures terrible performance. Lemire's algorithm innovation is that, in most cases, it does not need even 1 modulo.

However, if we know we will be generating numbers from the same distribution repeatedly, one of the modulos can be amortized as it depends purely on the distribution range (see part 1). The specialized implementation will require only one modulo per generated number, thus providing reasonable performance.

For use cases where we cannot amortize the first modulo for computing threshold, we can safely assume that this algorithm is not competitive.

Java

uint64_t java(uint64_t max) {
    uint64_t x = random64();
    uint64_t r = x % max;
    while (x - r > -max) {
        x = random64();
        r = x % max;
    }
    return r;
}

This algorithm needs on average 1 modulo per generated number, but it might require multiple. Unlike the OpenBSD and Lemire algorithms, there are no optimizations we can apply for generating multiple numbers from the same distribution^[2].

We should expect this to be about equal to the OpenBSD algorithm for generating many numbers in the same distribution, and much better for generating numbers from different distributions.

Benchmarks

Once again, all the benchmarking code is on GitHub. In fact, it is in the same repository. For this post, we have three different benchmarks:

1. Extended multiplication
2. Generating multiple random numbers from the same range
3. Generating random numbers from different ranges

Setup

Just as with the previous post, the numbers in this post were taken from my personal machine with a Ryzen 7 4750 CPU, but for this post, I am using slightly newer MSVC in version 19.39.33520 (this MSVC version comes installed with VS 17.9.1) and compiling for CMake-generated Release configuration^[3].

When benchmarking extended multiplication, we generate two arrays of varying sizes, multiply each pair, and sum the results to ensure that the computation is not optimized away. We do this because we cannot benchmark the multiplication of a single pair of numbers, as the overhead from Catch2's benchmarking becomes a significant part of the total runtime.

We use the same basic setup as in the previous part for the distribution benchmarks. There will be one benchmark where we generate a number from a different distribution every time and one where we generate many numbers from the same distribution. However, unlike the previous post, we do not attempt to model some real-world usage and instead look for bounds where Lemire's algorithm loses.

Because the previous post has shown that we can gain performance from specializing the implementation for generating multiple numbers from one distribution, I implemented each distribution in this post twice, once as standard for the no-reuse benchmark and once specialized for the reuse benchmark.

Results

All running time shown is in time per single element. You can click all images for a fullscreen version.

Extended multiplication

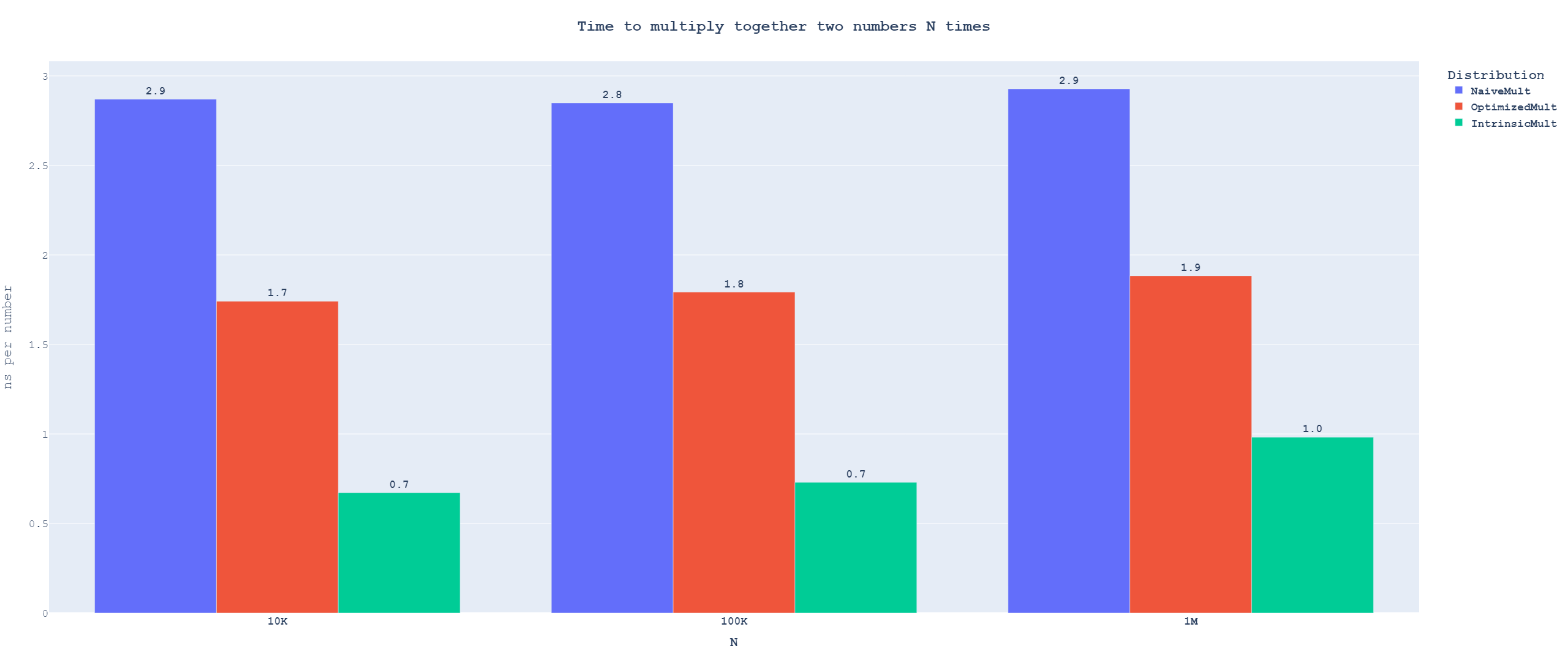You can also play around with the interactive version of the graph

We see some slowdown for long inputs. This slowdown is not interesting to us, as it is caused by running out of space in lower levels of cache, but in distribution code, we will only ever multiply two numbers at once. Looking at the results for small inputs, we see that using naive multiplication is more than 4 times slower than getting the compiler to "do the right thing" using intrinsics. Even if we optimize our implementation, there is still a 2.6x slowdown from using portable code.

This shows that other algorithms might be able to win if we do not use native 64x64 extended multiplication.

Single-use distributions

This is the case where we generate every number from a different range.

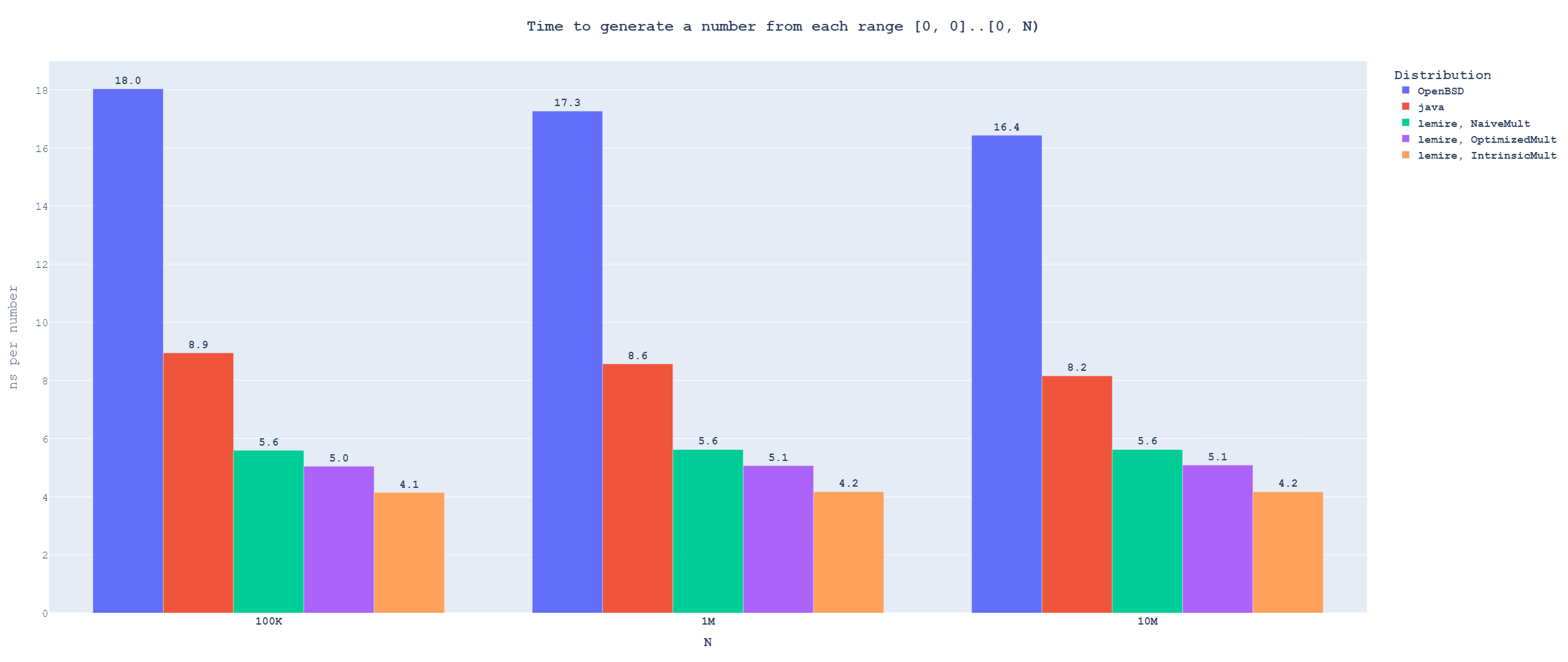You can also play around with the interactive version of the graph

As expected, the OpenBSD algorithm is not competitive for this use case. It takes roughly twice as long as the Java one because it pays the cost of the modulo twice per number. But Java is not competitive either. Lemire's algorithm is much faster even when it uses the naive extended multiplication implementation, and with the best extended multiplication implementation, it is roughly twice as fast.

Let's take a look at generating a lot of numbers from the same range instead.

Reused distributions

Updated 30.06.2024: I noticed a bug in the Java distribution implementation, which changed its performance profile. I reran the benchmarks and updated text below to reflect the reality.

This is the case where we generate a lot of numbers from the same range.

I originally collected a lot more data than is shown below, but I could not make the graph with all of them readable in image form. If you want to see the data in detail, here is an interactive graph.

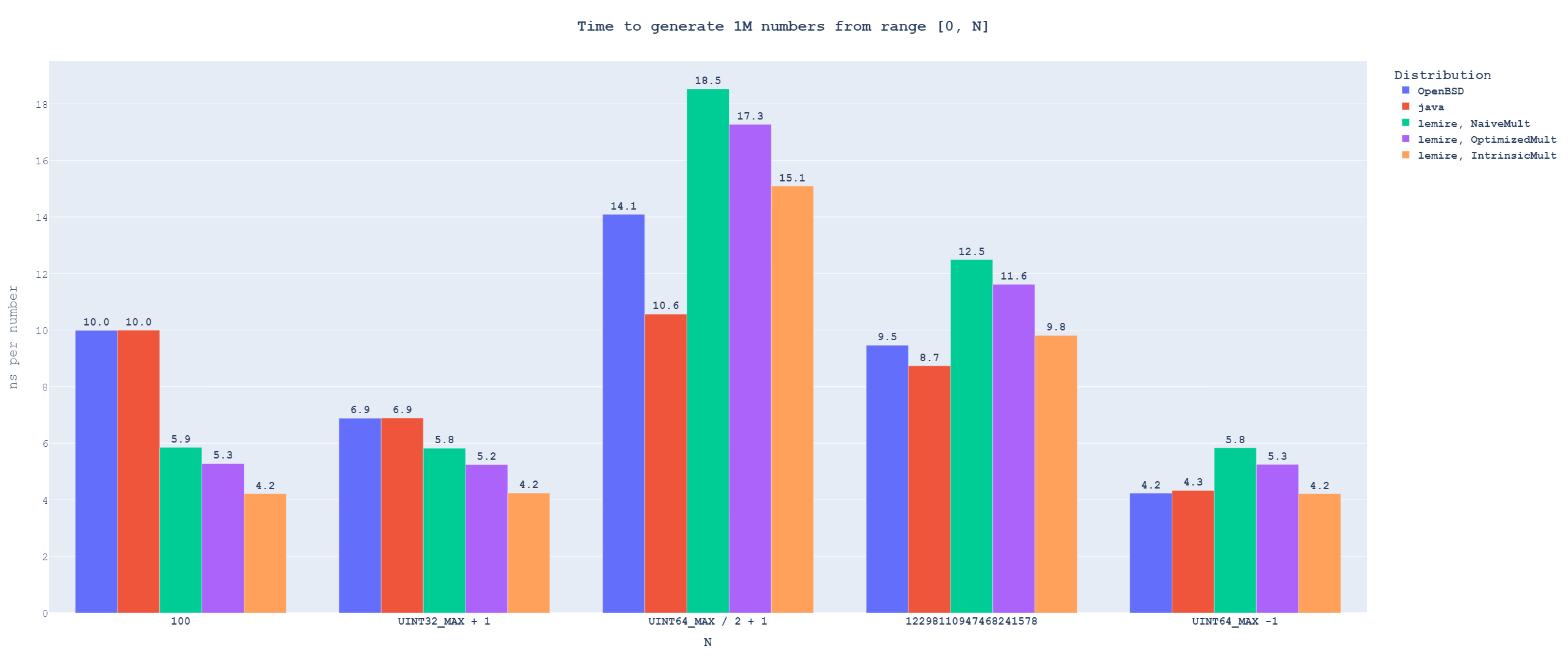You can also play around with the interactive version of the graph

The first thing we see here is that the time needed to generate one uniformly distributed number varies across different bounds. There are two reasons for this. The first is that the bounds change how many numbers from the underlying random number generators will be rejected^[4]. The second reason is that the DIV^[5] instruction has variable latency based on the input values.

Because Lemire's algorithm does not use modulo, the differences in its runtime come purely from the effect of rejection frequency. For N == UINT64_MAX / 2 + 1, each output from the random number generator has only \(\approx 50\%\) chance of being usable, which causes the massive spike there. Both OpenBSD and Java algorithms use modulo, and we can see that their runtime decreases^[6] even between bounds with roughly the same amount of rejection.

When we compare the distributions between themselves, we can see that the OpenBSD algorithm consistently wins over Java. This is a reversal of the results from the previous use case and is caused by the Java algorithm needing to compute one modulo per candidate number from a random number generator. In comparison, OpenBSD only needs one modulo per returned variate.

We can also see the OpenBSD algorithm slightly winning over Lemire's algorithm for specific, very high bounds. However, Lemire's algorithm is the better option for a generic use case, as it outperforms OpenBSD significantly for low bounds and performs equally or only slightly worse for high bounds.

The situation would be more complicated if we forced Lemire's algorithm to use portable extended multiplication. In this case, the OpenBSD algorithm achieves performance parity with Lemire's at lower bounds than against intrinsic extended multiplication and, for higher bounds, actually outperforms it.

Conclusion

In the shuffle-like workload, Lemire's algorithm outperforms both Java and OpenBSD algorithms by a significant margin. In fact, OpenBSD performs so badly for this workload type that if you have to pick a single algorithm for all your needs, you should never pick the OpenBSD algorithm.

The OpenBSD algorithm can outperform Lemire's when generating many numbers from the same, very large, range. However, the biggest measured win for OpenBSD is ~8%, while it loses by much bigger margins for small ranges, so Lemire's algorithm is the better workload-independent choice. However, we can gain performance by choosing and picking different algorithms based on the size of the range from which to generate. This links back to my old claim that an ideal <random> library should expose the different distribution algorithms under their names rather than under abstract names based on their statistical properties. Back then I based this opinion on allowing future extensions to the standard library, as people invent better algorithms to generate random numbers with specific properties, but these results provide another reason; usage-dependent performance differences.

That's it for this part. The next part will be about generating uniformly distributed floating point numbers and how different algorithms lead not just to different performance, but to fundamentally different generated numbers.