I recently realized that I could try to implement the reuse-oriented distributions from part 2 using libdivide instead of native division (modulo). This post will quickly go through the results of benchmarking this approach.

Introduction

If you are not familiar with libdivide, it is a library for optimizing integer division in workloads where you will be using the same runtime[1] divisor multiple times. libdivide does not support computing modulo, but we can fake it by substituting n % d for n - (n / d) * d.

In the distribution reuse workload from part 2, both the OpenBSD and the Java algorithm compute modulo using the same modulus every time, so precomputing a faster division has the potential to improve performance.

Benchmarks

For this post, I just extended the benchmark for generating many random variates from the same range from part 2. For more details, look there.

Results

As in part 2, all running time shown is in time per single element, and you can click all images for a fullscreen version. There is also once again a separate interactive graph with all data and distributions.

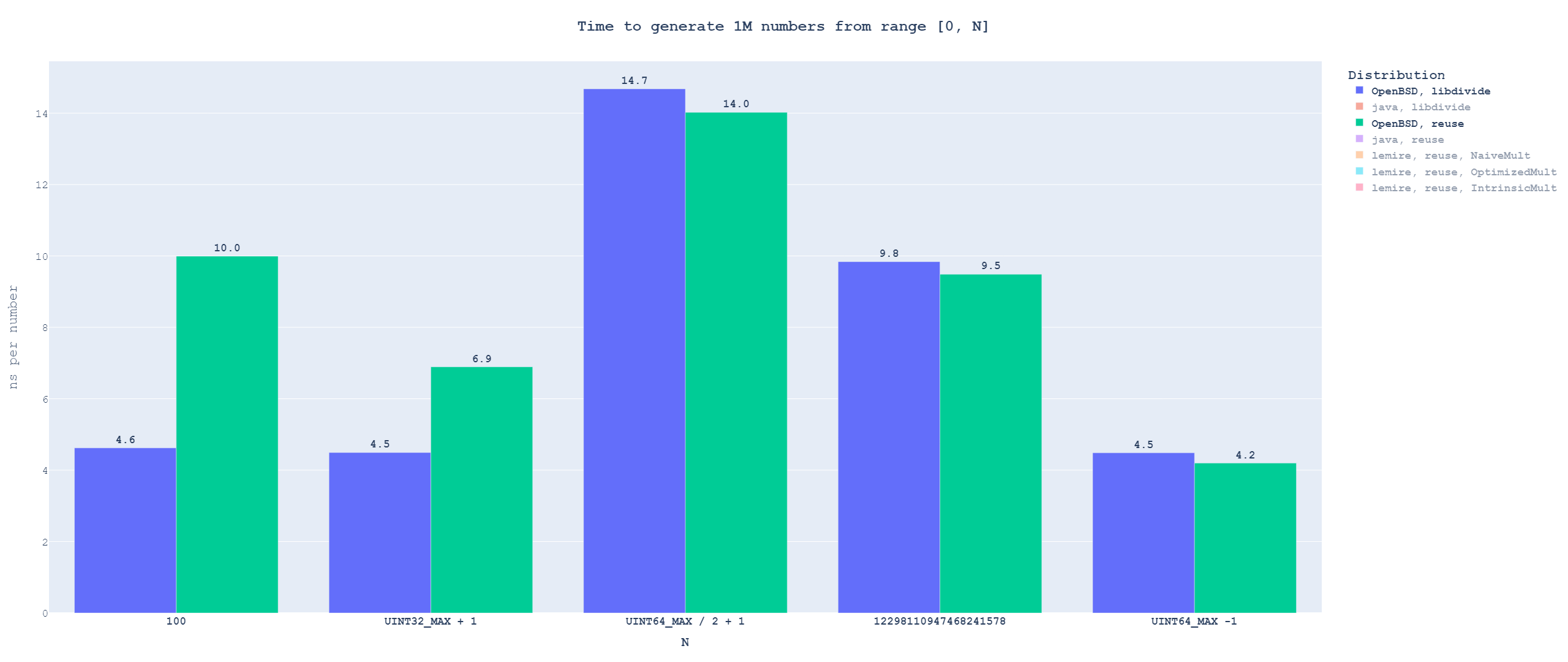
Bar graph with the time to generate many numbers from single distributions, OpenBSD with HW division vs OpenBSD with libdivide

Interestingly, using libdivide is not always better. It provides a significant speed-up for small ranges but is a slowdown for large ranges. This is interesting, because it means that for large divisors, the performance of the hardware divider is close to the performance of multiplication[2].

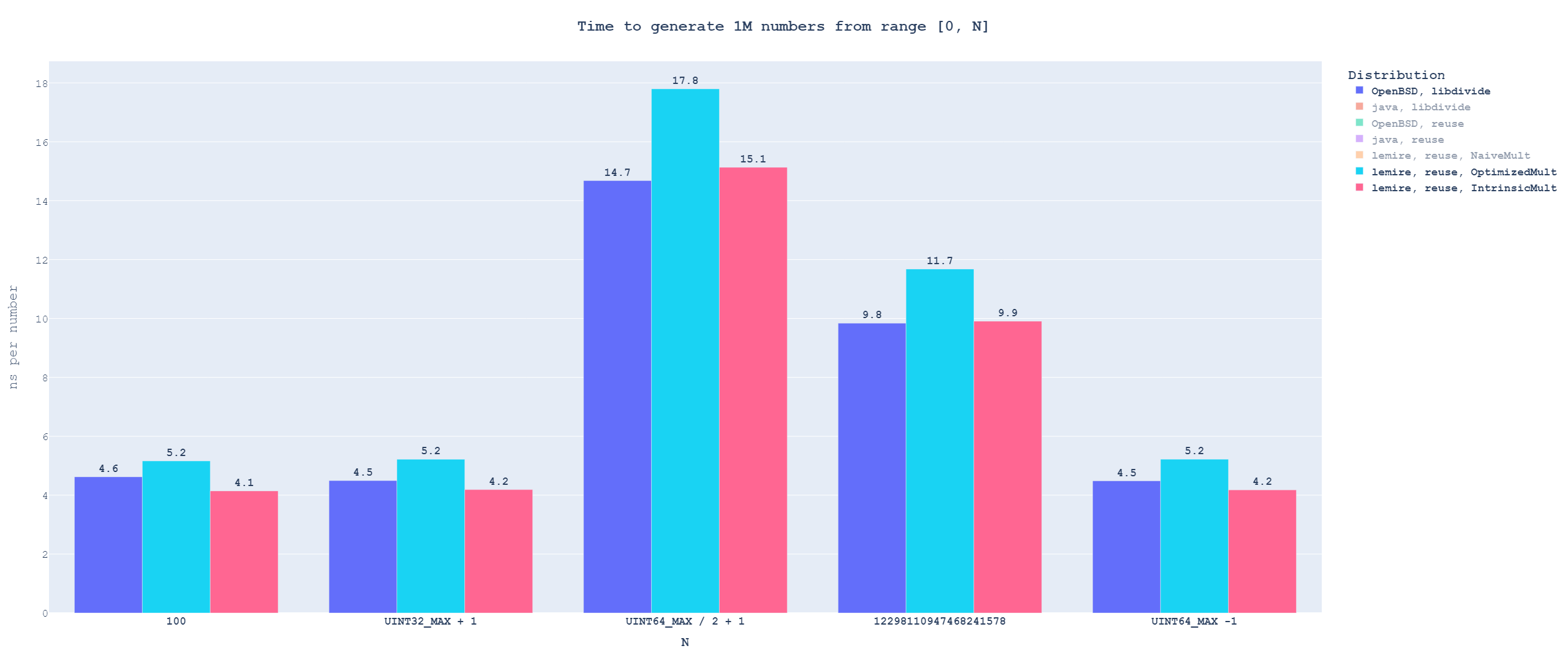
Bar graph with the time to generate many numbers from single distributions, OpenBSD with libdivide vs Lemire's algorithm

Compared to Lemire's algorithm, OpenBSD + libdivide no longer loses significantly for small ranges. But it also does not win by a meaningful margin for bigger ranges. Technically, it wins against Lemire's with slower multiplication, but that is a deeply unfair comparison; both algorithms now rely on 64x64->128 extended multiplication, so we cannot use slower implementation just for one of them.

Conclusion

Using libdivide is not a strict win for either OpenBSD or Java[3] algorithm. In a world where Lemire's algorithm does not exist, it would be an interesting improvement, as it evens out the performance differences between the different output range sizes.

However, Lemire's algorithm does exist, and using libdivide turns the OpenBSD algorithm into a worse Lemire's algorithm. OpenBSD + libdivide replaces the modulo operation with an extended multiplication, addition, shift, and another multiplication + subtraction. Lemire's algorithm uses a clever insight about extended multiplication + downshift to range reduce the generated random number directly.

  1. If the divisor is known at compile time, the compiler will optimize it for you. ↩︎

  2. libdivide works by doing extended multiplication between the input and a precomputed constant, followed by some adds and shifts to fix up the results[4]. For our use case, that is, taking modulo, we add extra multiplication and subtraction on top of this. ↩︎

  3. I did not talk about results from Java's algorithm in this post for a simple reason: it was worse for this use case in part 2, and using libdivide has changed nothing about the underlying reason for this. I included the data in the big graph, but the tl;dr is that using libdivide for Java's algorithm is the same as with OpenBSD: better performance for small ranges, worse performance for large ranges. ↩︎

  4. Does this sound weirdly familiar? It should; Lemire's algorithm is based around a similar emul + downshift trick to reduce the input range into a predefined range. ↩︎